�P�D�n�߂�
�u�Y���_�͐�������ΕK����A���q�b�g�����v
�Ƃ������ɉ������l������B
�܂��A�u��A���q�b�g����Y���_�A�����łȂ���Y���_�łȂ��v
�ƌ����l������B
���_���炢���ƁA�������S���̊ԈႢ�ł���B
�Ȃ��Ȃ�A���ۂɓG�@��������Y���_�r�[���̊Ԋu�́A
�������Y���_�ɂ����������ԂƂ͓������Ȃ�����ł���B
�܂��A�w�i�������̃Y���_���j�ߋ����̃Y���_�̕������܂�₷���x
�ƌ����邱�Ƃ�����B
����͊ԈႢ�ł͂Ȃ����A���m�Ȍ������ł͂Ȃ��B
���d�v�Ȃ̂́A�ˌ���ɐi�����ƁA�����ƓG
�@�̊p�x�ł���B
���̃y�[�W�ł́A�Y���_���������ɓG�@��������r�[���̊Ԋu��
�w�Y���_���x�Ƃ��ĕ\�����ɂ��A
�Y���_�������ɐ��l�����A�����̌������������ړI�Ƃ��Ă���B
�Q�D�Y���_���̓��o
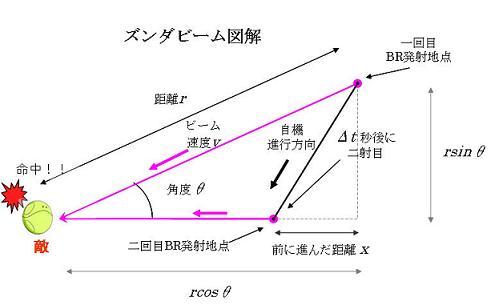
��
����ʑ��\������
�}�̂悤�ɃY���_��������Ԃ��l����B
��t
�i�f���^�� �j�͎��@�̈��ڂƓ��ڂ�BR�̎ˌ��Ԋu�A
�� ���� �͎��@�ƓG�@�̋����Ɗp�x�A
�� �͒��n����܂łɑO�ɐi�����ł���B
�܂��Av �̓r�[���̑��x�ł���B
���ڂ�BR�������Ă���G�ɓ�����܂ł̎��Ԃ́A
�G�܂ł̋�����BR�̑��x�Ŋ���悢�̂ŁA
t 1 = r/v ��
�\�����B
��}�̃s���N�F�̎ߐ����A���ڂ̃r�[���̐i�����ł���B
���ɁA���ڂ�BR�������Ă���G�ɓ�����܂ł̎��Ԃ��l���悤�B
�}�̐����ȃs���N�F�̐����A�r�[���̐i�����ł���B����xv
�Ŋ���ƁA
���̎��Ԃ�t 2 = (rcos��-x)/v
�ƂȂ�B
���ڂƓ��ڂ̎��@�̎ˌ��Ԋu����t �ł���̂ŁA
���ڂ̃r�[���Ɠ��ڂ̃r�[�����G�ɓ�����ԊuT �́A
t2 +��t
����At1 ���������߂���B���ۂɌv�Z����ƁA
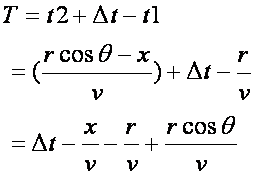
�ƂȂ�B���������ƁA
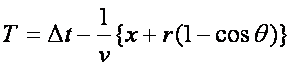
�ƂȂ�B������Y���_��T�@�ƌĂԂ��Ƃɂ���B
�����A�}�̒��p�O�p�`�̒�ӂ̕���rcos����d �ƒu���ƁA�Y���_��T �́A
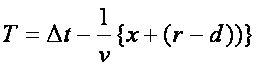
�Ə���������B
���̌`�̕����O�p��cos�Ƃ������邽�߁A
�����̐l�ɂƂ��Ă͗������₷����������Ȃ��B
�ǂ���̎������̈Ӗ��͓����ł���B
�R�D�Y���_�����番���鎖
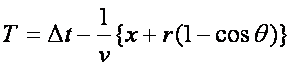
��̃Y���_���ɂ��ėǂ��l���Ă݂悤�B
���ۂɓG�̊�����r�[���̊ԊuT �͑�G�c�Ɍ����āA
�r�[���̎ˏo�Ԋu��t ���璆�J�b�R�o �p
�̒��g���������`�ɂȂ��Ă���B
���Ȃ킿�AT <��t�@�̊W�����藧���Ă�
��B
�Ⴆ�A�ő��̎ˏo�Ԋu��t �ŃY���_�������ł��A
��������Ƌ������l�߂Ă���ƁA�ő��̊Ԋu
�����Z���Ԋu
�ŃY���_�Ă邱�Ƃ��ł���B
�n�߂ɗ���������w�Y���_�͕K��������x�Ƃ����l���́A
�w���ۂɓG�@�̊�����ˌ��Ԋu�x���w���@�̃Y���_�̎ˏo�Ԋu�x
T =��t
�Ƃ���������琶�������̂��Ƃ��������킩��B
���ۂɂ́A���̓�͓������Ȃ��B
���ɁA�ǂ�����ΓG�@�̊�����r�[���̊ԊuT ���������Ȃ邩���l����B
�܂��Y���_���ɂ����āA��ԏd�v�ȍ�����t �ł���B
�Y���_�̒��ɂ��A�r�[���ƃr�[���̎ˏo�Ԋu���w�Z���x�Y���_�Ɓw�����x�Y���_������B
��t ���ˏo�Ԋu�̒Z���Y���_�̕�
���L���ł��鎖�������Ă���B
������O�ƌ����Γ�����O�ł���B
���ɁA�Y���_����x/v �̍��ɒ��ڂ���B
x �͈�˖ڂ����˖ڂ܂łɁi���������Ɂj�i��
���ł���B
���̍��́A�Y���_�����鎞�́A
�������l�߂������L���ł��邱�Ƃ�
��������B
�Ō�̍� r (1-cos��) �͒����I�ɕ������
�����`��������B
r �͎��@�ƓG�@�������̋����A���͎��@�ƓG�@�̊p�x�ł���B
r
�͐��������̋����i�O�̐}�̎O�p�`�̒�ӕ����j�Ƃ͈قȂ邱�Ƃɒ��ӁB
���̐��������̋�����d �ƒu�������A
r cos�� = d �Ȃ̂�
r (1-cos��) = (r - d)
�Ə�����B
����́w���@�ƓG�@�̋����x - �w���������̋����x�����̍��̐��̂ł��鎖�������Ă���B
(r - d)���A�w���p
�O�p�`�̎Ε��x - �w����x�Ə�����������ƍl���Ă��ǂ��B
���p�O�p�`�̎Εӂƒ�ӂ̍����傫���Ƃ��A���̍��͑傫�Ȓl�ƂȂ�A
�G�@�̊�����ˌ��ԊuT �����������邱�Ƃ��ł���B
��ӂ̒l��ς����ɁA�Εӂ̒l��傫������ɂ́A
�O�p�`�̊p�x����傫�����邩�A������傫������Ηǂ��B
���Ȃ킿�A�Y���_�����鎞��
��荂���ʒu����A�p�x��t���Ďˌ����������L����
����B
�n�߂ɗ���������A�w�������Y���_���ߋ����Y���_�̕����L���x�Ƃ����l���́A
�w���������x�Ō��Ȃ�w�ߋ����Y���_�̕����L���x
�Ə��������ΐ������B����́A
���������Ȃ�A�ߋ����̂ق����p�x���傫���Ȃ�L
��������ł���B
���� r (1-cos��)��r �ɒ��ڂ���ƁA
�p�x�������Ȃ�A����r
���傫���Ƃ��AT �͏������Ȃ�B
����́A��艓������ˌ����������L���ɂȂ鎖�������Ă���i�悤�Ɍ�����j�B
�������A���ۂɉ���������Y���_������ꍇ�A�p�x���͏������B
������Ɓ� 0 �ƌ��Ȃ��Ar
(1-cos��)��0�ɂȂ�B
���̎��A�Y���_���́A
T����t - x/v
�ƂȂ�A
�O�ɐi����x �݂̂�����ɂȂ��Ă���B
���������ł́A�ǂ����Ă��p�x�͏������Ȃ�A
�p�x�̕�͖w�ǎ��Ȃ��B�]���āA
�������ł́A�p�x�ȏ�ɑO�ɐi�������d�v��
����B
�e��v �ɒ��ڂ���� -1/v�~�o �p �̂悤�ȋt���̌`�����Ă���B
v ���������Ȃ�ƁA
1/v�~�o �p �̒l�͑傫���Ȃ�B
���Ȃ킿�A�e���̒x���@�̂̕����L���ł���B
�������ۂɂ́A�r�[���̑��x�͋@�̂��Ƃɑ傫���قȂ��ł͂Ȃ��̂ŁA
����قNjC�ɂ��Ȃ��Ă��悢���낤�B
4�D�Ō�ɂ��܂�
�_�b�V���������@�̂́A
�O�i����x �̕���傫���Ȃ�̂ŗL���B
�Y���_���ŁA�� = 0 �Ƃ���Ə��W�����v�Y���_�̏ꍇ�ɂȂ�B
���W�����v�Y���_��T ����t
�Ȃ̂ŁA�����Ɗp�x�̕��S���������Ȃ��B
�n�㖧���r�[�������W�����v���Y���_���n�������r�[���̂悤�ɁA
�����ŃY���_����Ίm��œ�����Ƃ����͉̂R�B�ő����͂��K�v�B
x = 0 �͓V�R�Y���_�i�^���ɗ�������Y���_�j�B
�p�x�݂̂�����B
�������ȏ�̓V�R�Y���_�́A�p�x����ꂸ�w�Ǖ�����Ȃ��B
�������ł�T����t - x/v
�ƍl���āA�قƂ�ǖ��Ȃ��B
�������ł̃Y���_�����܂�ɂ����@�́iZZ���C�t���A�M���v�����Ȃǁj�̏ꍇ�A
�_�b�V�����Ԃ����āA�O�ɐi�ދ���������Ɗm��q�b�g����悤�ɂȂ�B
����ł������Ȃ�A�Y���_�i���̂悤�ɁA�ڂ𖧒��V�C���Ɍ��ƃq�b�g����B
�������O�_�b�V�����Ԃ�����Ȃ�A��W�����v������Ȃ肵����ł̘b�B
�ߋ������ƁA�Y���_���̊p�x�̕���傫���Ȃ�A�Y���_���m��Ō��܂�₷���Ȃ�B
�Ō�܂œǂ�ł���Ă��肪�Ƃ��������܂����B
���̃y�[�W�̓����N�t���[�_���A�]�ڎ��R�ł��B
�����܂�
|

